考虑风向的GTWR

GTWR模型简介

一个回归问题

PM2.5数据的回归模型

$$pm2.5 = aod + wind + temperature + relativehumidity + hbpl$$

简化为

$$y = X_{aod} + X_{wind} + X_{temp} + X_{rh} + X_{hbpl}$$

OLS模型

在线性回归中，对于公式。

$$Y =X \beta + \epsilon$$ $$y=\begin{bmatrix} y_1\\ y_2\\ ...\\ y_n\\ \end{bmatrix} \quad \quad X=\begin{bmatrix} 1 & x_{11} & ... & x_{1p}\\ 1 & x_{21}& ... & _{2p}\\ ... & ...& ...& ...\\ 1 & x_{n1}& ... &x_{np} \end{bmatrix} \quad \quad \beta=\begin{bmatrix} \beta_0\\ \beta_1\\ ...\\ \beta_p\\ \end{bmatrix} \quad \quad \epsilon=\begin{bmatrix} \epsilon_0\\ \epsilon_1\\ ...\\ \epsilon_p\\ \end{bmatrix}$$

包含p个自变量，n条样本记录。

根据最小二乘法则，可得到

$$\hat\beta = (X'X)^{-1}X' y$$

由此，

$$\hat y=X\hat \beta=X (X'X)^{-1}X' y$$

其中，$H=X (X’X)^{-1}X’$ 称作为n*n的对称矩阵，也是幂等矩阵。

GWR模型

相比于OLS模型，改变了对于$\beta$的定义，认为$\beta$在每个位置都是不一样的，即

$$Y =(X \bigotimes \beta') I + \epsilon$$ $$\beta=\begin{bmatrix} \beta_{10} &... & \beta_{l0} & ... & \beta_{n0}\\ \beta_{11}&... & \beta_{l1} & ... & \beta_{n1}\\ ... & ...&...& ...& ...\\ \beta_{1p} &...& \beta_{lp} & ... & \beta_{np}\\ \end{bmatrix}$$

参照最小二乘原理，可得到

$$\hat\beta_i = (X'W_iX)^{-1}X'W_i y$$ $$\hat y_i=X_i\hat \beta_i=X (X'W_iX)^{-1}X'W_i y$$ $$w_i=\begin{bmatrix} w_{i1} &... & 0 & ... &0\\ 0&... &w_{i2} & ... & 0\\ ... & ...&...& ...& ...\\ 0&...& 0& ... & w_{in} \\ \end{bmatrix}$$

其中，这里的帽子矩阵为

$$S_i =X_i (X'W_iX)^{-1}X'W_i$$ $$S = [S_1,S_2...S_n]$$

空间权函数

W称作空间权函数，在样本点i上，都有其他所有点对i点的影响力，有距离阈值法、距离反比法、Gauss函数法、截尾型函数法等。总体都是随着距离而递减的函数，区间在[0,1]。

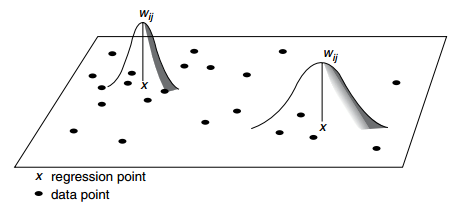
以某个权函数为例（高斯函数下图），带宽BandWidth的取值至关重要。

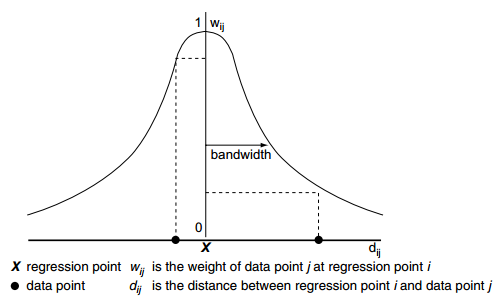
• 当带宽选取过大，即曲线很胖，则点周围大部分数据都具有较强的影响力，到无穷大时正好是OLS的模型。
• 当带宽选取过小，即曲线很瘦，则点周围大部分数据都不具备影响力，到无穷小是则每个点的影像取决于自己，此时$R^2=1$产生过拟合现象。

或者可以说：带宽过大回归参数估计的偏差过大，带宽过小又会导致回归参数的方差过大。

因此，不能通过R2最大化来寻找带宽值，而需要找到优化指标。有CV、AIC、BIC等。最常用的是AIC。

AIC准则

$$AIC=-2ln(\hat\theta_L,x)+2q$$

在gwr中，即为

$$AIC_c =2n\log_e(\hat\sigma)+n\log_e(2\pi)+n |\frac{n+tr(s)}{n-2-tr(s)}|$$

其中，$\hat\sigma$表示估计标准差，公式为

$$\hat\sigma=\sqrt{\frac{RSS}{n}}=\sum_{i}(y_i-\hat y_i)/(n-2v1_+v_2)$$

$v_1和v_2$ 值很相近，因此除数可以该做 $n-v_1$ 。 $v_1=tr(S)$ s表示帽子矩阵。$tr(s)$ 表示矩阵的迹。

GTWR模型

GWR考虑了数据空间上的影响，利用空间权函数W表示不同相邻空间距离间数据的影响力大小。

GTWR在此基础上，考虑数据在时空上的影像，将W改进为不同相邻时空距离间数据的影响力大小。

除此之外，没有任何区别。

因此，假设实现代码的话，只需要在对距离的定义函数上，从原先的空间距离dx+dy上，改成dx+dy+dt。

而时间和空间的尺度不一致，所以需要一个时空比例的参数Scale来衡量两者的权重大小。

即

$$距离=d^2x+d^2y+Scale*d^2t$$

Scale的确定

选取scale的区间，遍历任意一个scale，根据AIC准则获取最优带宽，从而得到R2。

依次遍历scale，获取R2最大下的scale。如下图所示。

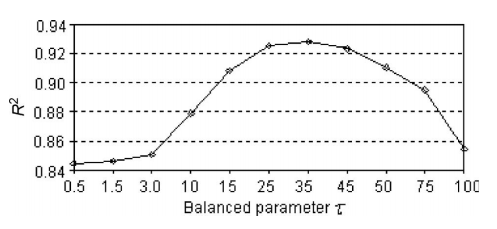
延伸

分析以上对线性模型的使用和改进，是针对GIS数据的特点，从传统的OLS模型，到考虑空间异质性，再到时空异质性的变化。

而对于异质性的研究，当前都是基于GIS第一定律：距离越近的越相似，距离越远的越不相似。可见，目前的研究改进主要集中在对距离概念的变换上。

但是，目前来说，对于距离各个方向都是均值的，即各向同性。如上述的每个空间权函数。

而实际上很多时候是各向异性的，需要考虑不同方向下的不同影响力。

风向影响就是一个很好的例子，对于空气污染扩散和蔓延来说，风向风速是既有影响力的相关因子，而简单地将WIND参数当做自变量放到线性模型中，往往无法获得较好的拟合结果，甚至相关性会非常差。

因此，需要考虑如何将风向影响结合到线性模型中，对于GWR及GTWR来说，风向对各个点产生的各向异性的影响力，就是一个可行的解决思路。